Resampling data

This notebook will demonstrate how to resample data with Lilio. Lilio is able to resample Pandas’ DataFrame and Series, as well as xarray’s DataArray and Dataset.

We start by importing the required libraries and generating an example Pandas Series and a DataFrame

import numpy as np
import xarray as xr
import pandas as pd
import lilio

time_index = pd.date_range('20171020', '20211001', freq='15d')
random_data = np.random.random(len(time_index))
example_series = pd.Series(random_data, index=time_index)
example_dataframe = pd.DataFrame(example_series.rename('data1'))
example_dataframe['data2'] = example_dataframe['data1']

example_series.head(3)

2017-10-20    0.053552
2017-11-04    0.314190
2017-11-19    0.291422
Freq: 15D, dtype: float64

The DataFrame looks similar but has two named columns:

example_dataframe.head(3)

	data1	data2
2017-10-20	0.053552	0.053552
2017-11-04	0.314190	0.314190
2017-11-19	0.291422	0.291422

To resample we need to set up an calendar with the anchor date and frequency. In this case we choose to use the daily_calendar shorthand.

(Passing max_lag is optional, as well as allow_overlap, but this will allow us to demonstrate that resampling works even when intervals overlap)

calendar = lilio.daily_calendar(
    anchor="10-15",
    length='90d',
    n_precursors=4,
    allow_overlap=True
)
calendar.map_years(2018, 2020)
calendar.visualize()

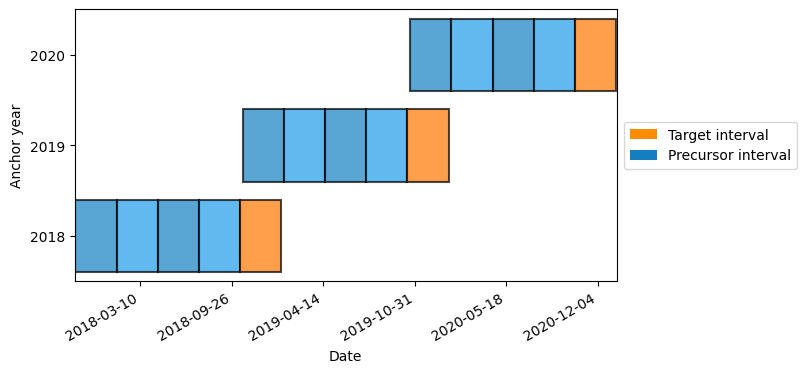
Next we pass the example data to the resample function. This requires a mapped calendar and the input data.

By default, resample will take the mean of all datapoints that fall within each interval. However, many other statistics are available, such as min, max, median, std, etc. For a full list see the docstring with:

help(lilio.resample)

resampled_series = lilio.resample(calendar, example_series, how="mean")
resampled_series

	anchor_year	i_interval	interval	data	is_target
0	2018	-4	[2017-10-20 00:00:00, 2018-01-18 00:00:00)	0.393967	False
1	2018	-3	[2018-01-18 00:00:00, 2018-04-18 00:00:00)	0.277288	False
2	2018	-2	[2018-04-18 00:00:00, 2018-07-17 00:00:00)	0.427301	False
3	2018	-1	[2018-07-17 00:00:00, 2018-10-15 00:00:00)	0.635698	False
4	2018	1	[2018-10-15 00:00:00, 2019-01-13 00:00:00)	0.369717	True
5	2019	-4	[2018-10-20 00:00:00, 2019-01-18 00:00:00)	0.378255	False
6	2019	-3	[2019-01-18 00:00:00, 2019-04-18 00:00:00)	0.487762	False
7	2019	-2	[2019-04-18 00:00:00, 2019-07-17 00:00:00)	0.508435	False
8	2019	-1	[2019-07-17 00:00:00, 2019-10-15 00:00:00)	0.323391	False
9	2019	1	[2019-10-15 00:00:00, 2020-01-13 00:00:00)	0.387587	True
10	2020	-4	[2019-10-21 00:00:00, 2020-01-19 00:00:00)	0.387587	False
11	2020	-3	[2020-01-19 00:00:00, 2020-04-18 00:00:00)	0.486544	False
12	2020	-2	[2020-04-18 00:00:00, 2020-07-17 00:00:00)	0.555756	False
13	2020	-1	[2020-07-17 00:00:00, 2020-10-15 00:00:00)	0.464762	False
14	2020	1	[2020-10-15 00:00:00, 2021-01-13 00:00:00)	0.487849	True

As you see above, this generates a new DataFrame containing the data resampled for each interval, along with the corresponding interval index, and the anchor year that the interval belongs to.

This works the same if you input a pandas DataFrame:

resampled_dataframe = lilio.resample(calendar, example_dataframe)
resampled_dataframe

	anchor_year	i_interval	interval	data1	data2	is_target
0	2018	-4	[2017-10-20 00:00:00, 2018-01-18 00:00:00)	0.393967	0.393967	False
1	2018	-3	[2018-01-18 00:00:00, 2018-04-18 00:00:00)	0.277288	0.277288	False
2	2018	-2	[2018-04-18 00:00:00, 2018-07-17 00:00:00)	0.427301	0.427301	False
3	2018	-1	[2018-07-17 00:00:00, 2018-10-15 00:00:00)	0.635698	0.635698	False
4	2018	1	[2018-10-15 00:00:00, 2019-01-13 00:00:00)	0.369717	0.369717	True
5	2019	-4	[2018-10-20 00:00:00, 2019-01-18 00:00:00)	0.378255	0.378255	False
6	2019	-3	[2019-01-18 00:00:00, 2019-04-18 00:00:00)	0.487762	0.487762	False
7	2019	-2	[2019-04-18 00:00:00, 2019-07-17 00:00:00)	0.508435	0.508435	False
8	2019	-1	[2019-07-17 00:00:00, 2019-10-15 00:00:00)	0.323391	0.323391	False
9	2019	1	[2019-10-15 00:00:00, 2020-01-13 00:00:00)	0.387587	0.387587	True
10	2020	-4	[2019-10-21 00:00:00, 2020-01-19 00:00:00)	0.387587	0.387587	False
11	2020	-3	[2020-01-19 00:00:00, 2020-04-18 00:00:00)	0.486544	0.486544	False
12	2020	-2	[2020-04-18 00:00:00, 2020-07-17 00:00:00)	0.555756	0.555756	False
13	2020	-1	[2020-07-17 00:00:00, 2020-10-15 00:00:00)	0.464762	0.464762	False
14	2020	1	[2020-10-15 00:00:00, 2021-01-13 00:00:00)	0.487849	0.487849	True

Resampling xarray data

Resampling works the same for an xarray Dataset. Note that you can use dask arrays as well, for lower memory use and distributed computation. For more info see the documentation.

Let’s make an example dataset with latitude and longitude coordinates:

import xarray as xr

time_index = pd.date_range('20171020', '20211001', freq='15d')

np.random.seed(0)
temperature = 15 + 8 * np.random.randn(2, 2, len(time_index))
precipitation = 10 * np.random.rand(2, 2, len(time_index))

lon = [[-99.83, -99.32], [-99.79, -99.23]]
lat = [[42.25, 42.21], [42.63, 42.59]]


ds = xr.Dataset(
    data_vars=dict(
        temperature=(["x", "y", "time"], temperature),
        precipitation=(["x", "y", "time"], precipitation),
    ),
    coords=dict(
        lon=(["x", "y"], lon),
        lat=(["x", "y"], lat),
        time=time_index,
    ),
    attrs=dict(description="Weather related data."),
)
ds

<xarray.Dataset> Size: 7kB
Dimensions:        (x: 2, y: 2, time: 97)
Coordinates:
    lon            (x, y) float64 32B -99.83 -99.32 -99.79 -99.23
    lat            (x, y) float64 32B 42.25 42.21 42.63 42.59
  * time           (time) datetime64[ns] 776B 2017-10-20 ... 2021-09-29
Dimensions without coordinates: x, y
Data variables:
    temperature    (x, y, time) float64 3kB 29.11 18.2 22.83 ... 7.116 3.225
    precipitation  (x, y, time) float64 3kB 5.25 7.506 3.335 ... 1.415 8.659
Attributes:
    description:  Weather related data.

xarray.Dataset

• Dimensions:
  • x: 2
  • y: 2
  • time: 97
• Coordinates: (3)
  • lon
    (x, y)
    float64
    -99.83 -99.32 -99.79 -99.23

    array([[-99.83, -99.32],
           [-99.79, -99.23]])

  • lat
    (x, y)
    float64
    42.25 42.21 42.63 42.59

    array([[42.25, 42.21],
           [42.63, 42.59]])

  • time
    (time)
    datetime64[ns]
    2017-10-20 ... 2021-09-29

    array(['2017-10-20T00:00:00.000000000', '2017-11-04T00:00:00.000000000',
           '2017-11-19T00:00:00.000000000', '2017-12-04T00:00:00.000000000',
           '2017-12-19T00:00:00.000000000', '2018-01-03T00:00:00.000000000',
           '2018-01-18T00:00:00.000000000', '2018-02-02T00:00:00.000000000',
           '2018-02-17T00:00:00.000000000', '2018-03-04T00:00:00.000000000',
           '2018-03-19T00:00:00.000000000', '2018-04-03T00:00:00.000000000',
           '2018-04-18T00:00:00.000000000', '2018-05-03T00:00:00.000000000',
           '2018-05-18T00:00:00.000000000', '2018-06-02T00:00:00.000000000',
           '2018-06-17T00:00:00.000000000', '2018-07-02T00:00:00.000000000',
           '2018-07-17T00:00:00.000000000', '2018-08-01T00:00:00.000000000',
           '2018-08-16T00:00:00.000000000', '2018-08-31T00:00:00.000000000',
           '2018-09-15T00:00:00.000000000', '2018-09-30T00:00:00.000000000',
           '2018-10-15T00:00:00.000000000', '2018-10-30T00:00:00.000000000',
           '2018-11-14T00:00:00.000000000', '2018-11-29T00:00:00.000000000',
           '2018-12-14T00:00:00.000000000', '2018-12-29T00:00:00.000000000',
           '2019-01-13T00:00:00.000000000', '2019-01-28T00:00:00.000000000',
           '2019-02-12T00:00:00.000000000', '2019-02-27T00:00:00.000000000',
           '2019-03-14T00:00:00.000000000', '2019-03-29T00:00:00.000000000',
           '2019-04-13T00:00:00.000000000', '2019-04-28T00:00:00.000000000',
           '2019-05-13T00:00:00.000000000', '2019-05-28T00:00:00.000000000',
           '2019-06-12T00:00:00.000000000', '2019-06-27T00:00:00.000000000',
           '2019-07-12T00:00:00.000000000', '2019-07-27T00:00:00.000000000',
           '2019-08-11T00:00:00.000000000', '2019-08-26T00:00:00.000000000',
           '2019-09-10T00:00:00.000000000', '2019-09-25T00:00:00.000000000',
           '2019-10-10T00:00:00.000000000', '2019-10-25T00:00:00.000000000',
           '2019-11-09T00:00:00.000000000', '2019-11-24T00:00:00.000000000',
           '2019-12-09T00:00:00.000000000', '2019-12-24T00:00:00.000000000',
           '2020-01-08T00:00:00.000000000', '2020-01-23T00:00:00.000000000',
           '2020-02-07T00:00:00.000000000', '2020-02-22T00:00:00.000000000',
           '2020-03-08T00:00:00.000000000', '2020-03-23T00:00:00.000000000',
           '2020-04-07T00:00:00.000000000', '2020-04-22T00:00:00.000000000',
           '2020-05-07T00:00:00.000000000', '2020-05-22T00:00:00.000000000',
           '2020-06-06T00:00:00.000000000', '2020-06-21T00:00:00.000000000',
           '2020-07-06T00:00:00.000000000', '2020-07-21T00:00:00.000000000',
           '2020-08-05T00:00:00.000000000', '2020-08-20T00:00:00.000000000',
           '2020-09-04T00:00:00.000000000', '2020-09-19T00:00:00.000000000',
           '2020-10-04T00:00:00.000000000', '2020-10-19T00:00:00.000000000',
           '2020-11-03T00:00:00.000000000', '2020-11-18T00:00:00.000000000',
           '2020-12-03T00:00:00.000000000', '2020-12-18T00:00:00.000000000',
           '2021-01-02T00:00:00.000000000', '2021-01-17T00:00:00.000000000',
           '2021-02-01T00:00:00.000000000', '2021-02-16T00:00:00.000000000',
           '2021-03-03T00:00:00.000000000', '2021-03-18T00:00:00.000000000',
           '2021-04-02T00:00:00.000000000', '2021-04-17T00:00:00.000000000',
           '2021-05-02T00:00:00.000000000', '2021-05-17T00:00:00.000000000',
           '2021-06-01T00:00:00.000000000', '2021-06-16T00:00:00.000000000',
           '2021-07-01T00:00:00.000000000', '2021-07-16T00:00:00.000000000',
           '2021-07-31T00:00:00.000000000', '2021-08-15T00:00:00.000000000',
           '2021-08-30T00:00:00.000000000', '2021-09-14T00:00:00.000000000',
           '2021-09-29T00:00:00.000000000'], dtype='datetime64[ns]')

• Data variables: (2)
  • temperature
    (x, y, time)
    float64
    29.11 18.2 22.83 ... 7.116 3.225

    array([[[29.11241877, 18.20125767, 22.82990387, 32.92714559,
             29.94046392,  7.18177696, 22.60070734, 13.78914233,
             14.17424919, 18.28478802, 16.15234857, 26.63418806,
             21.0883018 , 15.97340013, 18.55090586, 17.66939462,
             26.95263259, 13.35873389, 17.50454161,  8.16723409,
             -5.42391853, 20.22894876, 21.91548959,  9.06267984,
             33.15803699,  3.3650746 , 15.36606814, 13.5025292 ,
             27.26223371, 26.75487016, 16.23957941, 18.02530016,
              7.89771402, -0.84637175, 12.21670281, 16.25079175,
             24.84232545, 24.61903879, 11.90138546, 12.581578  ,
              6.61157628,  3.6398565 ,  1.34983847, 30.60620316,
             10.92278255, 11.49540559,  4.97763712, 21.21992285,
              2.08881722, 13.29807776,  7.83626751, 18.09521998,
             10.9135589 ,  5.55494253, 14.77454217, 18.42665496,
             15.53213778, 17.41977518,  9.92542325, 12.09807067,
              9.62031642, 12.12357471,  8.49482974,  1.18973918,
             16.41940914, 11.78575251,  1.95841322, 18.70225804,
              7.74161308, 15.41556317, 20.8327245 , 16.03186329,
             24.11520548,  5.12139344, 18.21873313,  9.52151927,
              8.03362281, 10.36920268, 12.50757974, 15.44932274,
    ...
             23.62195045,  5.98539353,  9.15457798, 11.92096153,
             15.75481271, 14.66262839, 12.70490246, 14.50698878,
             14.14155779,  9.24316489,  8.49605609, 17.19613086,
              7.87267934,  5.74115793, 12.50166199, 13.73866387,
             33.05378798,  9.36239779, 22.5460858 , 20.97750667,
              5.48844036, 21.18602382,  5.52895488, -6.2733779 ,
             19.85055619,  0.95287533, 18.60747569,  9.52791282,
             28.27640637, 23.54807519, 11.37291357,  9.49729911,
              5.28738078, 11.47261894, 12.75715604, 12.08245164,
             16.25363084, 19.62817198, 17.79723566,  8.88684861,
              3.49766821, 25.91625478,  9.48440652,  9.7816512 ,
             10.8304855 ,  0.2554436 , 11.17620797, 11.16275349,
             19.96286639, 20.58765719, 15.03016711, 22.45478699,
             17.71971987, 14.87454311, 16.28742535, 13.47477205,
             11.84120389, 12.8581317 ,  5.97590935, 17.24353364,
              7.05501111, 21.73305011, 13.00433136, 15.39595985,
             18.95069421, 20.14651572,  2.43501273, 13.34477059,
             22.0414313 ,  1.41515344, 18.0982438 , -3.04451384,
              6.81994525, 15.30904441,  1.74627918,  7.1159141 ,
              3.22531994]]])

  • precipitation
    (x, y, time)
    float64
    5.25 7.506 3.335 ... 1.415 8.659

    array([[[5.24970442e+00, 7.50595023e+00, 3.33507466e+00, 9.24158767e+00,
             8.62318547e+00, 4.86902960e-01, 2.53642524e+00, 4.46135513e+00,
             1.04627889e+00, 3.48475989e+00, 7.40097526e+00, 6.80514481e+00,
             6.22384429e+00, 7.10528403e+00, 2.04923687e+00, 3.41698115e+00,
             6.76242482e+00, 8.79234763e+00, 5.43678054e+00, 2.82699651e+00,
             3.02352580e-01, 7.10336829e+00, 7.88410351e-02, 3.72679070e+00,
             5.30537215e+00, 9.22111462e+00, 8.94945450e-01, 4.05942322e+00,
             2.43131997e-01, 3.42610984e+00, 6.22231059e+00, 2.79067948e+00,
             2.09749950e+00, 1.15703233e+00, 5.77140244e+00, 6.95270006e+00,
             6.71957141e+00, 9.48861021e+00, 2.70321389e-02, 6.47196654e+00,
             6.00392237e+00, 5.88739610e+00, 9.62770320e+00, 1.68716734e-01,
             6.96482431e+00, 8.13678650e+00, 5.09807197e+00, 3.33964870e+00,
             7.90840163e+00, 9.72429256e-01, 4.42035638e+00, 5.19952375e+00,
             6.93956411e+00, 9.08857320e-01, 2.27759502e+00, 4.10301563e+00,
             6.23294673e+00, 8.86960781e+00, 6.18826168e+00, 1.33461471e+00,
             9.80580133e+00, 8.71785735e+00, 5.02720761e+00, 9.22347982e+00,
             5.41380794e+00, 9.23306068e+00, 8.29897369e+00, 9.68286410e+00,
             9.19782811e+00, 3.60338174e-01, 1.74772004e+00, 3.89134677e+00,
             9.52142697e+00, 3.00028919e+00, 1.60467644e+00, 8.86304666e+00,
             4.46394415e+00, 9.07875594e+00, 1.60230466e+00, 6.61117512e+00,
    ...
             8.74399917e+00, 1.12427317e+00, 2.12434361e+00, 1.83033292e+00,
             4.03026002e+00, 7.45232960e+00, 5.26907449e+00, 4.87676324e+00,
             5.45964897e-03, 4.25401725e+00, 6.35537748e-01, 2.08253252e+00,
             9.32393939e+00, 2.15398204e+00, 8.58337639e+00, 8.02893372e+00,
             1.59146237e+00, 6.05711957e+00, 1.15661872e+00, 7.27888158e+00,
             6.37462277e+00, 8.11938562e+00, 4.79384549e+00, 9.14863088e+00,
             4.93489468e-01, 2.92888565e+00, 7.15052597e+00, 4.18109212e+00,
             1.72951354e+00, 1.07210745e+00, 8.17339111e+00, 4.73142978e+00,
             8.82283672e+00, 7.33289134e+00, 4.09726206e+00, 3.73511014e+00,
             5.15638347e+00, 8.89059953e+00, 7.37278580e+00, 5.15296427e-02,
             6.94157851e+00, 9.19507407e+00, 7.10455760e+00, 1.77005782e+00,
             4.83518127e+00, 1.40316018e+00, 3.58995278e+00, 9.37117042e+00,
             9.23305308e+00, 2.82836852e+00, 3.39631044e+00, 6.00212868e+00,
             9.63197295e+00, 1.47801334e+00, 2.56916644e+00, 8.73556827e+00,
             4.91892232e+00, 8.98961092e+00, 1.85517898e+00, 5.32668587e+00,
             3.26269633e+00, 3.16542560e+00, 4.46876964e+00, 4.33077449e+00,
             3.57346880e+00, 9.14970770e+00, 7.31744185e+00, 7.27546991e+00,
             2.89913450e+00, 5.77709424e+00, 7.79179433e+00, 7.95590369e+00,
             3.44530461e+00, 7.70872757e+00, 7.35893897e+00, 1.41506486e+00,
             8.65945469e+00]]])

• Indexes: (1)
  • time
    PandasIndex

    PandasIndex(DatetimeIndex(['2017-10-20', '2017-11-04', '2017-11-19', '2017-12-04',
                   '2017-12-19', '2018-01-03', '2018-01-18', '2018-02-02',
                   '2018-02-17', '2018-03-04', '2018-03-19', '2018-04-03',
                   '2018-04-18', '2018-05-03', '2018-05-18', '2018-06-02',
                   '2018-06-17', '2018-07-02', '2018-07-17', '2018-08-01',
                   '2018-08-16', '2018-08-31', '2018-09-15', '2018-09-30',
                   '2018-10-15', '2018-10-30', '2018-11-14', '2018-11-29',
                   '2018-12-14', '2018-12-29', '2019-01-13', '2019-01-28',
                   '2019-02-12', '2019-02-27', '2019-03-14', '2019-03-29',
                   '2019-04-13', '2019-04-28', '2019-05-13', '2019-05-28',
                   '2019-06-12', '2019-06-27', '2019-07-12', '2019-07-27',
                   '2019-08-11', '2019-08-26', '2019-09-10', '2019-09-25',
                   '2019-10-10', '2019-10-25', '2019-11-09', '2019-11-24',
                   '2019-12-09', '2019-12-24', '2020-01-08', '2020-01-23',
                   '2020-02-07', '2020-02-22', '2020-03-08', '2020-03-23',
                   '2020-04-07', '2020-04-22', '2020-05-07', '2020-05-22',
                   '2020-06-06', '2020-06-21', '2020-07-06', '2020-07-21',
                   '2020-08-05', '2020-08-20', '2020-09-04', '2020-09-19',
                   '2020-10-04', '2020-10-19', '2020-11-03', '2020-11-18',
                   '2020-12-03', '2020-12-18', '2021-01-02', '2021-01-17',
                   '2021-02-01', '2021-02-16', '2021-03-03', '2021-03-18',
                   '2021-04-02', '2021-04-17', '2021-05-02', '2021-05-17',
                   '2021-06-01', '2021-06-16', '2021-07-01', '2021-07-16',
                   '2021-07-31', '2021-08-15', '2021-08-30', '2021-09-14',
                   '2021-09-29'],
                  dtype='datetime64[ns]', name='time', freq='15D'))

• Attributes: (1)

  description :

  Weather related data.

As you see below, the temperature and precipitation variables can easily be resampled to a new index using the calendar specified intervals.

This index dimension has as coordinates the anchor year and the interval count.

Note: both the temperature and precipitation variables have kept their lat and lon coordinates.

ds_r = lilio.resample(calendar, ds)
ds_r

<xarray.Dataset> Size: 1kB
Dimensions:        (anchor_year: 3, i_interval: 5, x: 2, y: 2)
Coordinates:
  * anchor_year    (anchor_year) int64 24B 2018 2019 2020
  * i_interval     (i_interval) int64 40B -4 -3 -2 -1 1
    lon            (x, y) float64 32B -99.83 -99.32 -99.79 -99.23
    lat            (x, y) float64 32B 42.25 42.21 42.63 42.59
    left_bound     (anchor_year, i_interval) datetime64[ns] 120B 2017-10-20 ....
    right_bound    (anchor_year, i_interval) datetime64[ns] 120B 2018-01-18 ....
    is_target      (i_interval) bool 5B False False False False True
Dimensions without coordinates: x, y
Data variables:
    temperature    (anchor_year, i_interval, x, y) float64 480B 23.37 ... 12.55
    precipitation  (anchor_year, i_interval, x, y) float64 480B 5.74 ... 4.758
Attributes:
    description:                 Weather related data.
    lilio_version:               0.4.2
    lilio_calendar_anchor_date:  10-15
    lilio_calendar_code:         Calendar(\n    anchor='10-15',\n    allow_ov...
    history:                     2024-03-27 16:11:42 UTC - Resampled with a L...

xarray.Dataset

• Dimensions:
  • anchor_year: 3
  • i_interval: 5
  • x: 2
  • y: 2
• Coordinates: (7)
  • anchor_year
    (anchor_year)
    int64
    2018 2019 2020

    name :

    anchor year

    units :

    year

    description :

    The anchor date is the start of the period you want to forecast, and is an abstract date and does not include a year. Anchor years are used to create a full date with the anchor date (here: 10-15).

    array([2018, 2019, 2020])

  • i_interval
    (i_interval)
    int64
    -4 -3 -2 -1 1

    name :

    interval index

    units :

    -

    description :

    The index of each Lilio Calendar interval. Positive values denote intervals after the anchor date (targets), while negative values represent intervals before the anchor date (precursors).

    array([-4, -3, -2, -1,  1])

  • lon
    (x, y)
    float64
    -99.83 -99.32 -99.79 -99.23

    array([[-99.83, -99.32],
           [-99.79, -99.23]])

  • lat
    (x, y)
    float64
    42.25 42.21 42.63 42.59

    array([[42.25, 42.21],
           [42.63, 42.59]])

  • left_bound
    (anchor_year, i_interval)
    datetime64[ns]
    2017-10-20 ... 2020-10-15

    name :

    Left bound of the interval

    closed :

    True

    array([['2017-10-20T00:00:00.000000000', '2018-01-18T00:00:00.000000000',
            '2018-04-18T00:00:00.000000000', '2018-07-17T00:00:00.000000000',
            '2018-10-15T00:00:00.000000000'],
           ['2018-10-20T00:00:00.000000000', '2019-01-18T00:00:00.000000000',
            '2019-04-18T00:00:00.000000000', '2019-07-17T00:00:00.000000000',
            '2019-10-15T00:00:00.000000000'],
           ['2019-10-21T00:00:00.000000000', '2020-01-19T00:00:00.000000000',
            '2020-04-18T00:00:00.000000000', '2020-07-17T00:00:00.000000000',
            '2020-10-15T00:00:00.000000000']], dtype='datetime64[ns]')

  • right_bound
    (anchor_year, i_interval)
    datetime64[ns]
    2018-01-18 ... 2021-01-13

    name :

    Right bound of the interval

    closed :

    False

    array([['2018-01-18T00:00:00.000000000', '2018-04-18T00:00:00.000000000',
            '2018-07-17T00:00:00.000000000', '2018-10-15T00:00:00.000000000',
            '2019-01-13T00:00:00.000000000'],
           ['2019-01-18T00:00:00.000000000', '2019-04-18T00:00:00.000000000',
            '2019-07-17T00:00:00.000000000', '2019-10-15T00:00:00.000000000',
            '2020-01-13T00:00:00.000000000'],
           ['2020-01-19T00:00:00.000000000', '2020-04-18T00:00:00.000000000',
            '2020-07-17T00:00:00.000000000', '2020-10-15T00:00:00.000000000',
            '2021-01-13T00:00:00.000000000']], dtype='datetime64[ns]')

  • is_target
    (i_interval)
    bool
    False False False False True

    name :

    Target flag

    description :

    Denotes if an interval was marked as a target interval in the Lilio Calendar.

    array([False, False, False, False,  True])

• Data variables: (2)
  • temperature
    (anchor_year, i_interval, x, y)
    float64
    23.37 17.11 22.26 ... 14.28 12.55

    array([[[[23.36549446, 17.10623812],
             [22.26238524, 17.48205385]],
    
            [[18.60590392, 18.33568363],
             [15.22605039, 16.04933376]],
    
            [[18.93222815, 21.71327241],
             [15.86241907, 11.71770969]],
    
            [[11.90916256, 19.67654646],
             [14.10339232, 13.05611392]],
    
            [[19.9014688 , 13.99448977],
             [16.24401403, 13.5023425 ]]],
    
    
           [[[17.08172587, 17.92604246],
             [11.17720608, 12.29254973]],
    
            [[13.06441041, 15.27545014],
    ...
             [12.1541231 , 11.82364142]],
    
            [[11.74543481, 15.09573755],
             [13.84770432, 12.32257394]]],
    
    
           [[[11.74543481, 15.09573755],
             [13.84770432, 12.32257394]],
    
            [[13.83706304, 11.95144032],
             [13.65735477, 13.02433449]],
    
            [[ 8.66195308, 16.17757727],
             [10.23249271, 11.2407416 ]],
    
            [[17.13987126, 13.10521789],
             [11.8275895 , 17.81965851]],
    
            [[10.62867518, 16.4569909 ],
             [14.27640264, 12.55199757]]]])

  • precipitation
    (anchor_year, i_interval, x, y)
    float64
    5.74 4.722 3.611 ... 5.03 4.758

    array([[[[5.7404009 , 4.72163162],
             [3.61116044, 4.8505741 ]],
    
            [[4.28915654, 3.89836663],
             [1.36407099, 4.59694316]],
    
            [[5.7250198 , 4.12105515],
             [4.78924804, 6.73373353]],
    
            [[3.24585494, 6.27765595],
             [4.07517201, 3.8208838 ]],
    
            [[3.85834955, 7.46230301],
             [6.4563643 , 4.31465071]]],
    
    
           [[[4.01117262, 6.35335587],
             [6.35596951, 3.74886366]],
    
            [[4.24814754, 4.9843999 ],
    ...
             [3.28781693, 4.27202294]],
    
            [[3.4530543 , 4.08126979],
             [5.76219244, 5.70498641]]],
    
    
           [[[3.4530543 , 4.08126979],
             [5.76219244, 5.70498641]],
    
            [[6.08904131, 4.90265292],
             [5.86267549, 5.35799785]],
    
            [[7.65239785, 4.12167299],
             [3.88194967, 4.64966395]],
    
            [[5.73358736, 5.33329441],
             [7.49431035, 6.74383402]],
    
            [[4.76883618, 5.70610542],
             [5.02953315, 4.75774338]]]])

• Indexes: (2)
  • anchor_year
    PandasIndex

    PandasIndex(Index([2018, 2019, 2020], dtype='int64', name='anchor_year'))

  • i_interval
    PandasIndex

    PandasIndex(Index([-4, -3, -2, -1, 1], dtype='int64', name='i_interval'))

• Attributes: (5)

  description :

  Weather related data.

  lilio_version :

  0.4.2

  lilio_calendar_anchor_date :

  10-15

  lilio_calendar_code :

  Calendar( anchor='10-15', allow_overlap=True, mapping=('years', 2018, 2020), intervals=[ Interval(role='target', length='90d', gap='0d'), Interval(role='precursor', length='90d', gap='0d'), Interval(role='precursor', length='90d', gap='0d'), Interval(role='precursor', length='90d', gap='0d'), Interval(role='precursor', length='90d', gap='0d') ] )

  history :

  2024-03-27 16:11:42 UTC - Resampled with a Lilio calendar. See: https://github.com/AI4S2S/lilio

Calculating bin counts

To check if you have sufficient data for each of the Calendar’s intervals, you can make use of resample(how="size"). This will give you the number of data points that are within each interval.

Especially when the intervals are of varying sizes, or your data is more sparse, then this can be very useful.

As an example, let’s make a calendar with varyingly sized intervals:

calendar = lilio.Calendar(anchor="10-15")
calendar.add_intervals("target", length="5d")
calendar.add_intervals("precursor", length="1d")
calendar.add_intervals("precursor", length="3d")
calendar.add_intervals("precursor", length="10d")
calendar.map_years(2018, 2018)
calendar.visualize()

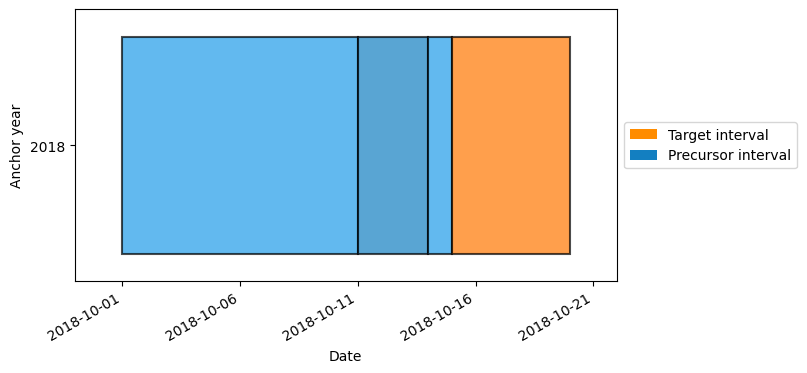
Now if we resample a dataset with a 1-day frequency, using how="size", you can see that the smallest interval contains only a single data point, while the largest interval contains ten.

Some of the resampling methods (such as “min” or “std”) of course would not make sense with such few data points per interval.

time_index = pd.date_range('20171020', '20191001', freq='1d')
random_data = np.random.random(len(time_index))
example_series = pd.Series(random_data, index=time_index)
example_dataframe = pd.DataFrame(example_series.rename('data1'))

lilio.resample(calendar, example_dataframe, how="size")

/home/docs/checkouts/readthedocs.org/user_builds/lilio/envs/latest/lib/python3.9/site-packages/lilio/utils.py:171: UserWarning:
  The input data frequency is very close to the Calendar's frequency.
  This could lead to issues like aliasing or incorrect resampling.
  If possible: make the Calendar's intervals larger, or use data of a
  higher time resolution.
  warnings.warn(
/home/docs/checkouts/readthedocs.org/user_builds/lilio/envs/latest/lib/python3.9/site-packages/lilio/utils.py:78: UserWarning:
  Some intervals only contains a single data point.
  This could lead to issues like aliasing or incorrect resampling.
  If possible: make the Calendar's intervals larger, or use data of
  a higher time resolution.
  warnings.warn(  # type: ignore

	anchor_year	i_interval	interval	data1	is_target
0	2018	-3	[2018-10-01 00:00:00, 2018-10-11 00:00:00)	10.0	False
1	2018	-2	[2018-10-11 00:00:00, 2018-10-14 00:00:00)	3.0	False
2	2018	-1	[2018-10-14 00:00:00, 2018-10-15 00:00:00)	1.0	False
3	2018	1	[2018-10-15 00:00:00, 2018-10-20 00:00:00)	5.0	True

Custom resampling methods

The how argument also accepts any function with a single input and a single output argument. This allows you to use custom defined functions to resample the data.

For example:

def root_mean_squared(data):
    return np.mean(data ** 2) ** 0.5

lilio.resample(calendar, example_dataframe, how=root_mean_squared)

/home/docs/checkouts/readthedocs.org/user_builds/lilio/envs/latest/lib/python3.9/site-packages/lilio/utils.py:171: UserWarning:
  The input data frequency is very close to the Calendar's frequency.
  This could lead to issues like aliasing or incorrect resampling.
  If possible: make the Calendar's intervals larger, or use data of a
  higher time resolution.
  warnings.warn(
/home/docs/checkouts/readthedocs.org/user_builds/lilio/envs/latest/lib/python3.9/site-packages/lilio/utils.py:78: UserWarning:
  Some intervals only contains a single data point.
  This could lead to issues like aliasing or incorrect resampling.
  If possible: make the Calendar's intervals larger, or use data of
  a higher time resolution.
  warnings.warn(  # type: ignore

	anchor_year	i_interval	interval	data1	is_target
0	2018	-3	[2018-10-01 00:00:00, 2018-10-11 00:00:00)	0.516371	False
1	2018	-2	[2018-10-11 00:00:00, 2018-10-14 00:00:00)	0.714292	False
2	2018	-1	[2018-10-14 00:00:00, 2018-10-15 00:00:00)	0.363845	False
3	2018	1	[2018-10-15 00:00:00, 2018-10-20 00:00:00)	0.686525	True